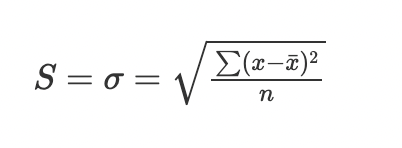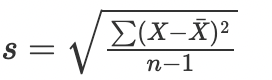Measures of Dispersion
Data has a pattern of distribution. It is usually not concentrated in one area but dispersed or scattered. The mean is not useful to measure this scattering. This scattering can be captured using the measures of dispersion. The mean can be seen as a fixed point from which the dispersion can be measured either in absolute terms or relative terms.
Absolute Measures of Dispersion
When the measures of dispersion are measured in the same units that the data is measured, we call it absolute dispersion. We do so using the range, mean absolute deviation, and standard deviation.
Range
The range is the difference between the largest and smallest unit in the distribution. If R is the range, L is the largest variable, and S the smallest, then R= L - S. The range can be calculated for closed frequency distributions where the limits are clearly defined. The range can be calculated for grouped and ungrouped data.
Ungrouped data
6,18, 54, 76, 86, 21
R = L - S
Therefore R = 86 -6, i.e 80.
Grouped data
| Kms walked per month | Number of people |
|---|---|
| 10 to 25 | 15 |
| 25 to 40 | 10 |
| 40 to 55 | 3 |
| 55 to 70 | 1 |
Upper limit is 70 and the lower limit is 10. The range is therefore 70-10 or 60.
Mean Absolute Deviation
The mean absolute deviation is the average of the absolute values of the difference between each observation and the arithmetic mean.
First, the arithmetic mean for the dataset is calculated. Then the difference between each data set value and the mean is calculated in absolute terms. Then the arithmetic mean for these deviations is calculated.